Diferența cheie: Un punct este un punct care denotă o locație care a fost marcată pe un spațiu infinit sau o suprafață plană. O linie este considerată a fi unidimensională și a fost introdusă pentru a reprezenta obiecte drepte fără lățime și adâncime. Un plan este o suprafață plană bidimensională, care este pe o durată nedefinită, cu grosime zero.
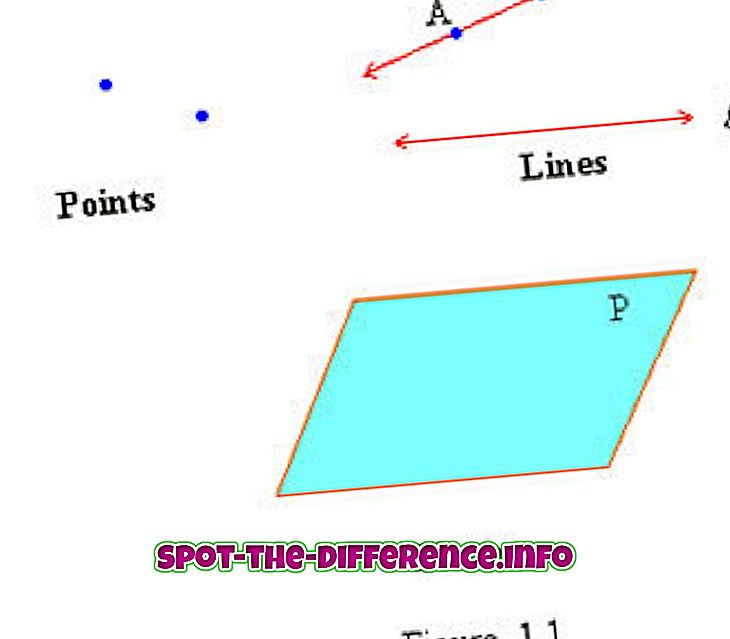
Punctul, linia și planul sunt considerate a fi termeni nedefiniți de geometrie deoarece nu sunt definiți formal. Atunci când definim un termen, de obicei folosim cuvinte mai simple pentru a descrie termenul. Cu toate acestea, un punct, o linie și un avion sunt considerate termeni deja simplificați. Toate celelalte concepte geometrice sunt construite pe punct, linie și avion. Totuși, să încercăm să înțelegem acești trei termeni nedefiniți.
Un punct este un punct care nu denotă nimic, ci o poziție. Punctul reprezintă o locație care a fost marcată în spațiul infinit sau pe o suprafață plană. Un punct poate fi un punct de orice dimensiune, dar nu are nici o lungime, lățime sau grosime. Acest lucru se datorează faptului că reprezintă un loc și nu un lucru.
Punctele sunt numite folosind o singură literă superioară, cum ar fi A, B, C etc. În spațiul euclidian bidimensional, mai bine cunoscut ca o rețea sau un grafic cu axa x și axa y, un punct este reprezentat de un ordonată pereche (x, y). X reprezintă plasarea orizontală a punctului, în timp ce y reprezintă plasarea verticală. Există două seturi de puncte: Collinear și coplanar. Setul colinar de puncte se află într-o linie dreaptă, în timp ce un set coplanar de linii se află pe același plan.
O linie este considerată a fi unidimensională și a fost introdusă pentru a reprezenta obiecte drepte fără lățime și adâncime. Definiția liniei se modifică în funcție de tipul de geometrie. În geometria Euclid, linia nu are definiție definită. În geometria analitică, o linie în plan este definită ca un set de puncte ale căror coordonate satisfac o ecuație liniară dată. În geometria incidenței, o linie poate fi un obiect independent din setul de puncte care se află pe ea.
O linie este acceptată ca un set infinit unidimensional de puncte care sunt conectate. O linie dreaptă este cea mai mică distanță dintre două puncte dintr-un plan. Linile sunt marcate cu două săgeți la sfârșitul fiecăruia, pentru a însemna că nu se termină niciodată. Linile sunt numite în două moduri: cu două puncte pe linie sau cu o singură literă cursivă cu litere mici. Orice două puncte marcate pe o linie pot fi folosite pentru a se referi la o linie. De exemplu: O linie cu punctele H, I pe ea va fi eticheta linie HI și o va fi plasat pe partea de sus a acesteia pentru a indica că este o linie.
Un plan este o suprafață plană bidimensională, care este pe o durată nedefinită, cu grosime zero. Un plan este considerat ca un analog bidimensional al unui punct (dimensiuni zero), o linie (una-dimensiune) și o solidă (tridimensională). Când se ia în considerare definiția în termeni de spațiu euclidian, planul se referă la întregul spațiu. Imaginați-vă o foaie de metal care nu are nici o grosime, totuși, ea continuă pentru totdeauna și vreodată. Acesta este considerat un avion.
Wikipedia afirmă că "multe sarcini fundamentale în matematică, geometrie, trigonometrie, teorie grafică și grafică sunt realizate într-un spațiu bidimensional sau cu alte cuvinte în plan". Deși planurile sunt infinite, de dragul tragerii, ele necesită margini. Aceste planuri sunt desenate de două perechi paralele și arată ca un dreptunghi înclinat. Planul are două dimensiuni: lungimea și lățimea. Dar, deoarece avionul este infinit de mare, lungimea și lățimea nu pot fi măsurate.
Avioanele sunt definite prin trei puncte. Există două tipuri de planuri: planuri paralele și planuri intersectate. Avioanele paralele sunt două sau mai multe planuri care merg infinit fără a se călca în calea celuilalt. Imaginați-vă foaia de metal anterioară, adăugați acum o altă foaie de metal care se află pe partea de sus a acesteia și continuă, de asemenea, pentru totdeauna. Aceste două ar face două planuri paralele care nu se intersectează niciodată. Cu toate acestea, avioanele interesante sunt exact așa. Acestea sunt două planuri care se încrucișă reciproc. Avioanele sunt numite în mod obișnuit cu o singură literă de majuscule scrisă în cursivă (planul P).
În geometrie, punctul, linia și planul sunt unite sub forma unui postulat. Acest postulat este o colecție de trei ipoteze (axiome) care pot fi folosite ca parte a unei baze pentru geometria euclidiană în trei sau mai multe dimensiuni. Cele trei ipoteze includ: ipoteza unică a liniei, ipoteza liniei de număr și ipoteza dimensiunii. Ipoteza unică a liniei sugerează că există exact o linie care trece prin două puncte distincte. Ipoteza liniei de numere indică fiecare linie este un set de puncte care pot fi puse într-o corespondență unu-la-unu cu numerele reale. Orice punct poate corespunde cu 0 (zero) și orice alt punct poate corespunde cu 1 (unul). În cele din urmă, ipotezele privind dimensiunile sunt date cu o linie într-un plan, există cel puțin un punct în planul care nu este pe linie. Având în vedere un plan în spațiu, există cel puțin un punct în spațiu care nu este în plan.